En el anterior post hablé de la radiación electromagnética y de alguna de sus utilidades prácticas, intentando desmitificar todo lo que existe en torno al electromagnetismo. Hoy toca hablar de uno de los usos más interesantes de las ondas electromagnéticas: la transmisión de información.
Seguiré con el ejemplo del post anterior: el mando a distancia. Vimos como efectivamente de él salía “luz”, pero quedaba sin responder la pregunta con la que cerraba el artículo: ¿cómo es que la televisión sabe después si has pulsado el 3, el 5, el 8 o lo que sea?
Para responder esta pregunta conviene estudiar algunas de las características de las ondas que nos pueden ayudar. Empezaremos con la amplitud. Imaginemos que tenemos un altavoz que sólo emite un sonido (un pitido). Todo el rato el mismo. Pero sin embargo, tenemos también un modulador que nos permite subir y bajar el volumen del altavoz desde un 0% hasta un 100% de su capacidad (siendo 0% silencio y 100% lo más alto). Una forma muy sencilla de transmitir información con este altavoz sería aclarar previamente con el receptor que si el sonido está entre 0% y 10% significa 0, entre 10% y 20% significa 1, entre 20% y 30% significa 2, y así hasta entre 90% y 100% que significará 9.
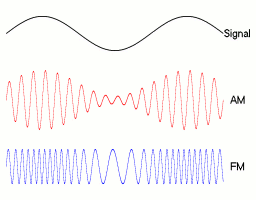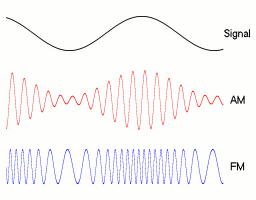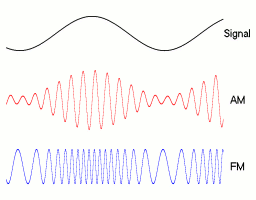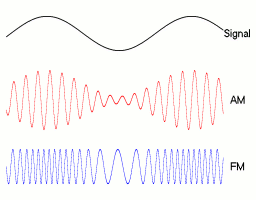
Con este sencillo método podríamos construir ya un mando a distancia un poco rudimentario pero funcional. Si quiero pulsar el 5, no tendría más que poner el altavoz a un valor entre el 50% y el 60% de su capacidad, y el receptor, que en este caso sería un micrófono, lo interpretaría y daría a la tele la orden de cambiar de canal. Esto es lo que se llama Amplitud Modulada (AM).
Estudiemos ahora el otro caso: la Frecuencia Modulada (FM). Volviendo con el altavoz, ahora nuestro altavoz lo que mantendría constante es la amplitud, es decir, el volumen, y lo que variaría es su frecuencia, es decir, el sonido (pitido) que emite. Así, el “micrófono” receptor tendrá ahora que comprobar qué pitido se ha emitido y después revisar en su “tabla de equivalencias” qué canal corresponde a ese pitido concreto. En la imagen siguiente se pueden observar cuatro ondas diferentes que varían entre sí la frecuencia y mantienen la misma amplitud.
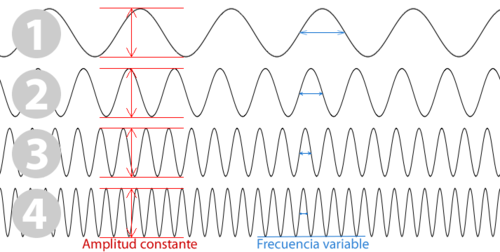
Aquí tienes los pitidos equivalentes a cada una de esas ondas (en orden del 1 al 4):
Si ahora en vez de variar la frecuencia de una onda de presión (sonido) variamos la frecuencia de una onda electromagnética, lo que obtendremos serán diferentes “colores”, aunque en muchos casos estos “colores” no serán visibles para el ojo humano. Es decir, es como si el mando fuera una linterna que puede emitir varios colores: el rojo, verde, azul, amarillo… y cada uno de ellos el receptor lo interpretara como un número.
Un ejemplo muy claro de transmisión de información por frecuencia y además de forma acústica es el teléfono. Probablemente te hayas dado cuenta de que cada número tiene un pitido asociado (realmente son dos). Antiguamente, antes de la “revolución digital”, el número al que el cliente quería llamar se determinaba así: la central recibía esos soniditos y en función de cuáles fueran te ponían en contacto con el terminal adecuado. De hecho, como todo se realizaba mediante pitidos, existía un “hack” que permitía hacer llamadas gratis intercontinentales tan sólo silbando con un silbato que regalaban en las cajas de cereales y que casualmente emitía a la frecuencia adecuada.
Sin embargo, quizás hayas observado que pulsando en uno u otro botón del mando sigues viendo el mismo “color” en la pantalla de tu móvil, en vez de ver tonos diferentes para cada número: esto sucede porque la variación de frecuencia entre un número y otro es muy pequeña, es decir, es como si cogiéramos diferentes tonalidades de rojo muy similares entre sí pero realmente diferentes, que sólo pudieran apreciarse con aparatos de medición sofisticados.
La Amplitud Modulada y la Frecuencia Modulada (AM/FM) son las formas “fundamentales” de transmitir información. No sólo a través del vacío mediante ondas electromagnéticas (desde tu móvil hasta una antena) sino también a lo largo de conductores (cables, como el USB o los propios chips de tu móvil), aunque sobre esto profundizaremos más en la tercera entrega, sobre electrónica.
Por ahora, todo lo expuesto ha sido muy esquemático y muy rudo, y la realidad (ya) no es así, todo es bastante más complejo, no sólo desde el punto de vista electrónico (de llevar todas estas ideas a los chips y las antenas y hacer que funcione), sino desde el punto de vista conceptual.
Sí que es verdad que siempre puedes establecer una “tabla de equivalencias” que diga “frecuencia de 1000Hz significa A, 1001Hz significa B,…” y así todo el abecedario, de forma que pudieras enviar cualquier mensaje simplemente emitiendo las frecuencias adecuadas. Pero eso tiene dos problemas: es lento, y las pérdidas de información pueden ser brutales.
Aquí es donde entra el concepto de “ruido”. Para entenderlo bien, simplemente podemos hacer una analogía con lo que todo el mundo comprende por ruido. Si tú estás hablando con alguien que está, pongamos, a 10metros de ti, y de pronto comienza a haber ruido, puede que a tu receptor no le llegue la información, o puede que directamente te entienda otra cosa completamente diferente.
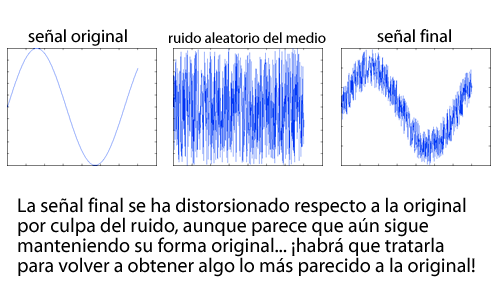
Pues con la información que va por medios electromagnéticos (cables, ondas electromagnéticas…) pasa exactamente lo mismo. Puede existir ruido en el medio que modifique la señal, aunque sea levemente. Y eso, si estabas mandando cosas muy precisas, puede ser desastroso.
Para evitar esto existe toda una teoría matemática, en la que hay mucha estadística (evidentemente, ya que el ruido es aleatorio) que habla sobre transmisión, compresión y procesado de información. Su precursor fue Claude Shannon, quien en 1948 publicó un estudio titulado “Una teoría matemática de la comunicación”. De esa teoría nacen los conceptos de compresión de datos, encriptación, y en general todo lo que está relacionado con tratar la información.
En cuanto a compresión de datos, realizaremos un sencillo ejemplo, sin perder de vista que los métodos usados en realidad son mucho más complicados. Cualquier vídeo, fotografía o sonido que escuches en un medio digital ha sido con toda probabilidad comprimido previamente, en formatos tan conocidos como AVI, JPG o MP3.
Imaginemos esta cadena de información que queremos transmitir: “AAAAAYTRBBBBCCCXZ”. En total ocupa 17 caracteres (llamémosles bytes). Resulta que yo podría tratar dicha cadena y simplificarla a “5AYTR4B3CXY”: ahora esta cadena ocupa 11 bytes y la información es exactamente la misma, solo que se transmitirá más rápido (aunque luego habrá que “descodificarla”). Este es un caso de compresión sin pérdidas, ya que la señal que volvemos a obtener es igual que la original. Existen otros formatos de compresión en el que hay pérdidas, es decir, la señal que obtenemos no es igual a la original, pero a efectos prácticos da igual porque se pierden datos inapreciables por los sentidos. Ejemplos de compresión con pérdidas son el JPG para imagen o el MP3 para sonido.
Otro ejemplo radica en la “redundancia”, es decir, la repetición de información no necesaria. Esto suele suceder mucho en los idiomas. Así, la frase “Me apetece cenar una hamburguesa con patatas” transmite la misma información que “M aptc cnar 1 ambrguesa cn patats”, y la segunda ocupa menos. (Nota: no estoy apoyando la destrucción al lenguaje, esto sólo era un ejemplo).

Sin embargo, a veces la intención de algunos sistemas no es reducir la redundancia sino aumentarla, ya que se conoce que el medio por el que se va a transmitir o donde se va a almacenar la información puede generar muchas pérdidas, por lo que “repitiendo” el mensaje te aseguras de que llegará con una probabilidad más alta. Un ejemplo muy claro de ello es el CD de toda la vida. ¿Nunca te has preguntado por qué ese CD que tiene unos rayajos bastante considerables todavía funciona? Un rayajo de un CD supone una pérdida de millones de bits de información, y sin embargo verás que probablemente siga escuchándose (hasta cierto punto, evidentemente). Todo porque existe información redundante a propósito. Lo curioso es que incluso redundando información que previamente has comprimido, el resultado puede ocupar menos bytes que el original sin comprimir…
La teoría de la información es muchísimo más amplia y compleja, pero a resumidas cuentas consiste en aprender a tratar la información desde un punto de vista matemático para aumentar la efectividad y eficiencia. Me he dejado conceptos clave para esta teoría como la entropía, que espero poder explicar en artículos venideros. Habiendo introducido muy básicamente la transmisión de información y la importancia de las matemáticas para tratarla, cierro aquí esta segunda entrega. La tercera, sobre electrónica.
Esta entrada pertenece a la serie de artículos Por qué escogí Teleco sobre divulgación científica relacionada con el campo de la Ingeniería de Telecomunicación.