Siempre nos han dicho y ha resultado ‘evidente a nuestro intelecto’ que la suma tiene la propiedad conmutativa, es decir, podemos cambiar el orden de sumandos y llegar al mismo resultado [5+3+2=2+5+3]. Ahora, ¿es esto así siempre?
Te propongo un pequeño ejercicio.
Imaginemos una ristra infinita de 1’s y otra de -1’s.
Tendríamos:
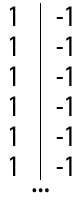
Ahora sumemos esas ristras por filas. En la primera fila (y en todas) tendremos 1+(-1), por lo que es fácil ver que siempre tendremos 0 como resultado (1-1+1-1+1-1…) por muchas filas que cojamos, incluso siendo éstas infinitas.
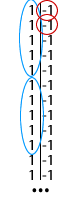
Utilicemos ahora la propiedad conmutativa. Según ésta, da igual como coja los elementos que vaya a sumar, siempre obtendré el mismo resultado. Es decir, si tengo para sumar el 8, el 5 y el -3 me da lo mismo coger primero 8+5 y luego sumar el -3, o cualquier otra combinación. Pues bien, ahora me da a mí la gana de coger primero cinco elementos de la primera ristra y luego uno de la segunda, como se observa en la imagen (por cada círculo azul, cojo uno rojo):
Es decir, iré sumando primero cinco de la primera ristra (1+1+1+1+1) y luego otro de la segunda (-1). Y haré eso tantas veces como quiera, ya que las ristras son infinitas.
No hace falta pensar demasiado para ver que sumando de esa forma no obtendremos el mismo resultado que sumando por filas (el cero). Es más, obtendremos un valor cada vez mayor que tenderá a +infinito.
¿Qué está pasando?