Sobre ceros y unos. Entendiendo la información digital.

Seguro que has escuchado un montón de veces que, en electrónica, al final todo son ceros y unos. Que si tu ordenador funciona con ceros y unos, que si la información que mandas (ya sea por internet, por teléfono o lo que sea) son ceros y unos, etcétera.

En este post pretendo aclarar, utilizando como ejemplo el teléfono, cómo se codifica la información para pasar de la voz que emites a una ristra de 0’s y 1’s que se puedan transmitir por un cable. Encontrarás algunos términos que te resultarán familiares, como los famosos bits, la expresión kbps y algunos más.

Para ello, en primer lugar, conviene tener presente cómo funciona el sistema binario. En binario, solo existen dos números: el cero y el uno. En decimal tenemos el 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9, y después de llegar al nueve empezamos a combinar los números que tenemos. Simplemente volvemos a empezar con el 0, solo que esta vez le añadimos un 1 delante… 10, 11, 12, etcétera.

¿Qué pasa en binario? Que empezamos a contar y muy pronto nos quedamos sin números: 0, 1,… ¿y ahora? Pues hacemos exactamente igual que en decimal. Ponemos un cero y delante un 1, de forma que queda 10 (se lee “uno cero” y no diez). Después vendrá el 11, y después el 100. Es decir, para contar desde el 0 hasta el 9 tendremos: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001… y así podremos ir formando absolutamente cualquier número que nos dé la gana.

Dicho esto, ya podemos aventurarnos a explicar cómo transformar nuestra voz, una canción, o cualquier señal analógica en algo digital compuesto por 0’s y 1’s.

Para esto, tomaremos como ejemplo una señal temporal como puede ser un sonido. Para apreciar correctamente el proceso, vamos a coger un período de tiempo de esta señal realmente pequeño: 0.001 segundos. Vamos, un milisegundo.

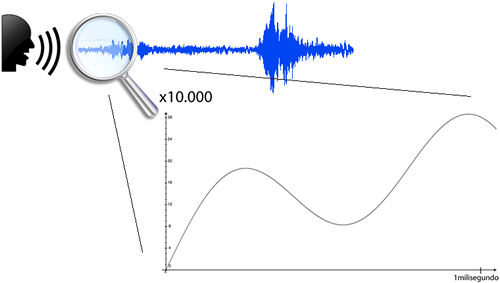
Lo primero que tenemos que hacer con nuestra señal es muestrearla. ¿Qué significa eso? Significa que cada un cierto período de tiempo nos vamos a ir quedando con el valor de la señal en ese instante. En nuestro caso muestrearemos con una frecuencia de muestreo 8000 Hz (Herzios), es decir, cada segundo vamos a tomar 8000 muestras (el teléfono funciona así). Haciendo un símil para entenderlo, es como si tuviéramos una cámara de fotos y cada segundo hiciésemos 8000 fotos. La razón de muestrear a 8000 Herzios tiene que ver con el teorema de Nyquist-Shannon, que establece que para la total recuperación de una señal se debe muestrear a, como mínimo, dos veces la frecuencia máxima de dicha señal. Pero como este es un tema demasiado complejo y no necesario para comprender esto, no entraremos en detalle.

Si dividimos un segundo entre 8000 muestras, nos dará que necesitamos coger una muestra cada 0.000125 segundos o, dicho de otro modo, cada 125 microsegundos (un microsegundo es la milésima parte de un milisegundo). Si recordamos que íbamos a trabajar con un período de 0.001 segundos, nos daremos cuenta de que en dicho período habrá exactamente 8 muestras, y a cada muestra le corresponderá un determinado valor, como puede observarse en la imagen a continuación.

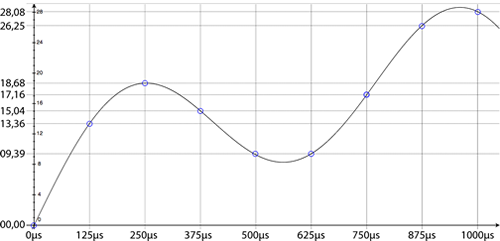
Como ya habrás empezado a sospechar, teniendo tantos valores va a ser bastante probable que después podamos volver a escuchar el sonido, ya que pasa como en el cine, donde al final la película son fotos que pasan muy rápido dando la ilusión de movimiento.

Ahora ya hemos muestreado, pero los 0’s y 1’s aún no se ven por ninguna parte. Lo que toca es “redondear” las muestras. Como habrás observado, a cada intervalo de tiempo le corresponde un valor numérico. Al 125microsegundos le corresponde el 13.3628, al 250microsecs el 18.6815, etc. Lo que debemos hacer es “redondear” este valor, o asignarle un número dependiendo el rango al que pertenezca. Vamos, que para todos los números que estén entre el 13 y el 14 nos quedaremos con un determinado número (en este ejemplo, y por simplicidad, escogeremos el 13). De forma que ahora el 125microsegundos quedará asociado al 13, el 250microsecs al 18, etcétera.

Y ahora es cuando, por fin, entra en juego el sistema binario. Esos números enteros ya los podemos transformar a números binarios. Cabe destacar que, por cada número, usaremos 8 bits. Vamos, que añadiremos el número necesario de ceros para llegar a 8 dígitos. Ejemplo: el número 5 en binario es 101, que quedaría: 00000101. Si nos damos cuenta, esto limita el número de valores a 256, ya que empezaríamos desde el 00000000 hasta el 11111111 (que en decimal es 255).

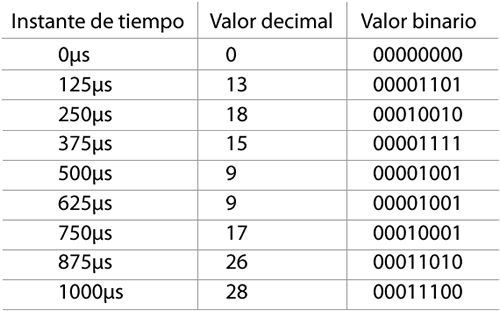
Ahora toca “crear” la nueva señal, sabiendo que cada 125 microsegundos tendremos que mandar los 8 bits de información correspondientes. Es decir, en el intervalo de tiempo desde 0 hasta 125 microsegundos, mandaremos 00000000 (ya que la primera muestra se toma en t=0 y en este caso equivale a 00000000). Después tendremos que mandar el 13, que es: 00001101, etcétera. Al hacer todas las conversiones y ponerlo todo seguido, tendríamos esto:

Que en forma de señal sería algo parecido a lo que se ve en la imagen a continuación:

Y así ya habríamos pasado nuestra señal de analógico a digital. Para recuperar la señal tendríamos que hacer el proceso inverso, aunque lógicamente no la recuperaremos exactamente igual a como era, ya que habremos perdido parte de la información sobre todo al cuantificar y redondear.

También cabe destacar, por último, la velocidad de bits por segundo. Podemos observar que si cada segundo tenemos 8000 muestras y cada muestra la hemos codificado con 8 bits, al final tendremos, en un segundo, 64000 bits, es decir, 64kbps (64kilo bits por segundo), que es la velocidad a la que va el teléfono (y aproximadamente a la que iba internet cuando nos conectábamos vía telefónica). Hay que darse cuenta que hay una diferencia entre un bit y un byte, ya que un byte son 8 bits… y con esto muchas veces nos engañan las operadoras. Si te dicen que tendrás 8Mb por segundo, te están diciendo que descargarás a una velocidad máxima de 8 millones de bits por segundo… es decir, 1 millón de bytes. Y resulta que los exploradores te dan la velocidad de bajada en bytes, en vez de en bits. Por eso, si tu operador te ofrece 8Mbps, la velocidad máxima que tú verás al descargar lo que sea será 1MB/sec. La diferencia en nomenclatura es que el bit va con minúscula (“b”) y el byte con mayúscula (“B”). Vamos, 8Mb=1MB.