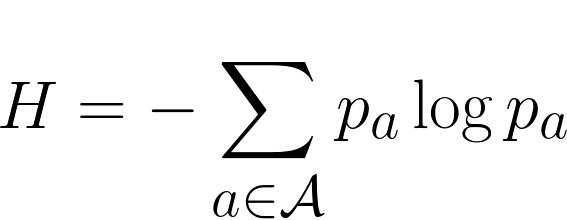
Probablemente este sea un post de barbaridades, algo así como la máquina de movimiento perpetuo, pero es algo a lo que le he estado dando vueltas últimamente y quería escribirlo. Está fuera de la divulgación típica del blog, eso sí.
Si tenemos una fuente de información, un cálculo exacto de la entropía (imposible en la mayoría de los casos, por otra parte) nos dará hasta dónde podemos comprimir la información. Pero este cálculo es esencialmente probabilístico, es decir, nos da una media cuando el número de elementos tiende a infinito.
Y lo más seguro es que esa sea precisamente la clave y la idea que realmente rompió con lo que había hasta entonces; dejar de tratar los casos de forma particular y empezar a utilizar modelos basados en probabilidad que te aseguraban que en un tiempo largo aquello funcionaría bien.
Sin embargo, a la hora de la verdad uno suele desconocer el modelo estadístico que ha generado la información y evidentemente las secuencias no son infinitas. Por poner un ejemplo muy tonto y a todas luces imposible, si uno tiene una fuente binomial que saca 0s y 1s con 50% de probabilidad, la entropía te dirá que necesitarás 1bit por elemento, y sin embargo puede darse el caso de que toque un run de 0s muy largo. Vale que cuando la secuencia sea muy grande el run de 0s no será una secuencia típica y por tanto su probabilidad de aparición será 0, y que aunque pase una vez no pasará las otras 100.000 cuatrillones de veces y por lo tanto comprimiendo así te irá mal, pero reitero que aquí no hablo para nada de tendencia a infinito ni medias sino de casos particulares.
Generalizando, imaginemos una secuencia de bits de la que no conocemos el modelo de la fuente que los ha generado. Lo cierto es que hay infinitas formas de obtener esa misma secuencia. Quizá si haces un desarrollo discreto de Fourier consigas unos coeficientes que se pueden comprimir con menos bits, o quizá haya una función matemática que muestreada cada k sus valores entren dentro de un rango mapeable a la secuencia, quizá si mapeas la secuencia resulta que obtienes los primeros 50 decimales de pi o de la raíz de 2, o quizá exista un modelo que, aunque no sea el de la fuente original, para ese caso particular se ajuste mejor.
En todos esos casos puede que estés comprimiendo por debajo de la entropía. No estás violando nada, ya que la entropía es una media y puede haber casos particulares que la mejoren, pero entonces la pregunta es: ¿se puede decir algo sobre estas funciones? ¿se puede asegurar al menos algún caso en el que existan? ¿se puede establecer que para una secuencia particular existirá siempre un modelo con una entropía menor al modelo original?
Yo me imagino que incluso aunque alguna de estas preguntas tuviera lógica y/o respuesta, lo más probable es que no haya forma de calcular tales funciones/modelos. Además, si fuera el caso y siempre pudieras encontrar un modelo para una secuencia, en teoría podrías ir comprimiendo infinitas veces, lo cual no parece tener mucha lógica, a no ser que fuera de forma asintótica, aunque suena bastante tonto. Y si fuera posible, en la práctica tendrías que indicar el modelo cada vez, y esto aumentaría el número de bits. ¿Conclusión? Ninguna, como siempre.