Hoy toca la famosa transformada de Fourier. ¿Qué es la transformada de Fourier? ¿qué tiene que ver con las famosas frecuencias de las que se habla constantemente? ¿A qué se refiere un DJ cuando dice que va a “amplificar los bajos”? Aquí pretendo dar un pequeño barniz divulgativo para aclarar qué es una transformada de Fourier, ya que todo lo que tiene que ver con frecuencias (ya sean las usadas en electromagnetismo o las sonoras) está directamente relacionado con esto y un conocimiento superficial es algo casi obligado por razones de cultura básica. Si quieres enterarte bien te recomiendo leer todo (no es una lectura densa) y prometo que acabarás sabiendo más o menos de qué va el asunto…
Para comprender la transformada, imaginemos en primer lugar una señal temporal de audio. Aunque igual te suena raro, seguro que has visto alguna señal de este tipo alguna vez, son las típicas que se van dibujando cuando hablas por un micrófono y que suben mucho si gritas. En estas gráficas el eje de abscisas (eje X, el horizontal) representa el tiempo mientras que el de ordenadas representa la presión del aire (que es como se mide el sonido).
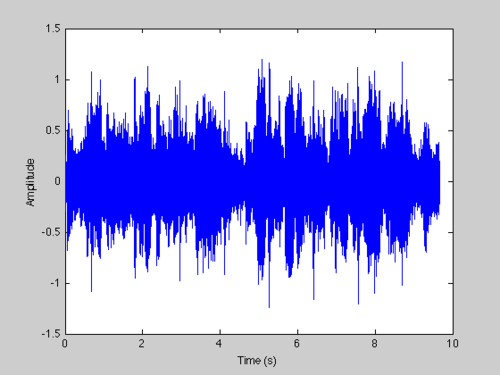
Esta es una forma gráfica de ver un sonido (tu voz, una canción, …) Sin embargo, también habrás oído hablar de “amplificar los bajos” o “filtrar no sé qué frecuencias” y cosas así. Aquí es donde entra la transformada de Fourier.
La transformada convierte nuestra señal de un “mundo” a “otro” y después podemos volver de este otro mundo al primero. Haciendo un símil con la música, es como estar en la clave de sol y pasar a clave de fa. Ahora las notas estarán en distintas posiciones pero sonarán igual.
En este caso, y mediante un operador matemático (la transformada propiamente), pasamos del “mundo” temporal al “mundo” frecuencial. Ahora nuestra señal, que cuando estábamos en el mundo temporal tenía una forma, tendrá otra distinta, y en el eje X, en vez de tener valores del tiempo, tendremos valores de frecuencia (que no se miden en segundos sino en Herzios). Pero lo importante es que la información contenida ¡sigue siendo exactamente la misma, solo que ahora la vemos de otra forma! Nuestra señal/función temporal se ha “re-escrito” de otra forma, pero siempre podremos volver a la original.
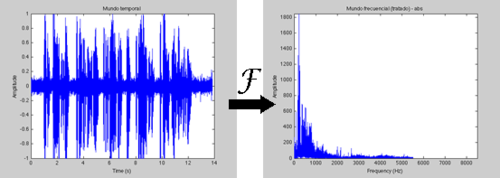
¿Por qué hacer esto, entonces? ¿Por qué “re-escribir” nuestra señal en este nuevo mundo? La gracia es que este mundo frecuencial nos aporta información de una forma mucho más clara, y por eso se utiliza tanto. En la gráfica anterior podríamos decir de forma inmediata que el sonido emitido tiene más frecuencias bajas que altas, por ejemplo.
Lo que en el mundo temporal equivaldría a una nota musical que suena indefinidamente (el LA, por ejemplo) en el mundo frecuencial supondría simplemente un pico a la frecuencia equivalente de ese LA. Si ahora tocamos a la vez el DO, MI, SOL y SI, algo que en el mundo temporal sería una señal con una forma rara, en el mundo frecuencial serían simplemente cuatro picos a las frecuencias correspondientes a DO, MI, SOL y SI.
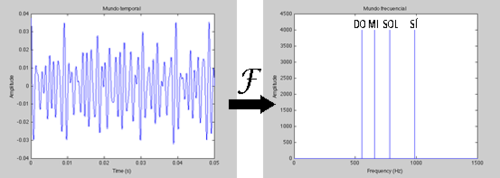
Si ahora tenemos toda una partitura, que vistas en el mundo temporal serán una locura, en frecuencia veremos perfectamente qué frecuencias está utilizando esa partitura. ¿Para qué sirve esto? La utilidad más inmediata es para tratar la señal, “jugar” con ella, en plan DJ. Si nosotros de esa partitura queremos eliminar los bajos (los sonidos más graves) podríamos pasar la señal (mediante matemáticas) al mundo frecuencial (el de Fourier), poner en cero las bajas frecuencias, después volver al mundo temporal y al escuchar la canción de nuevo, veríamos que los sonidos más bajos han desaparecido.
Ejemplos
Dado este audio:
Veamos primero su señal temporal y su transformada de Fourier:
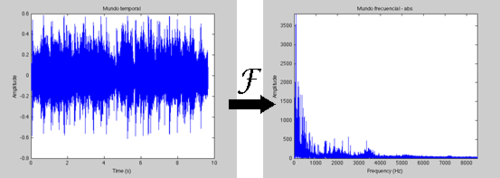
Ejemplo 1 – Eliminando las frecuencias bajas
Para esto, cojo mi señal de la transformada, y quito las frecuencias bajas, como puede verse en la siguiente imagen (¡así de fácil!)
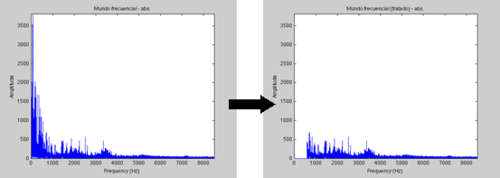
Después vuelvo del mundo frecuencia al mundo temporal, y tendré una señal completamente distinta a la original.
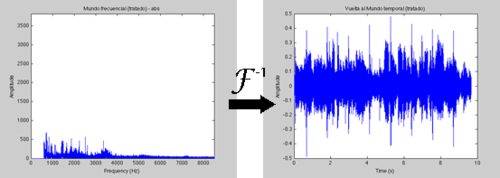
Donde F-1 significa transformada inversa, es decir, pasamos del mundo frecuencia al mundo temporal.
Si escucho esa nueva señal, oiré esto:
Ejemplo 2 – Amplificando bajas frecuencias
Ahora me interesa amplificar las bajas frecuencias, es decir, que éstas se escuchen más. Para ello, cogeré todas las frecuencias desde 0 hasta 430 Hz y las multiplicaré por cuatro, tal que así:
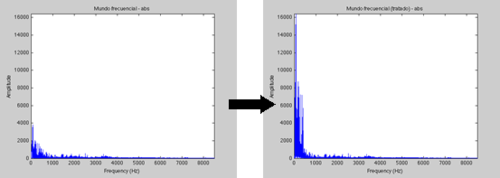
Haciendo ahora la transformada inversa, obtendremos esta señal temporal:
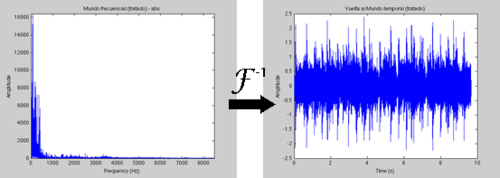
Que suena tal que así:
Ejemplo 3 – Escuchando las bajas frecuencias
Por último, vamos a quedarnos solamente con las frecuencias más bajas (de 0 a 430Hz), haciendo el resto cero.
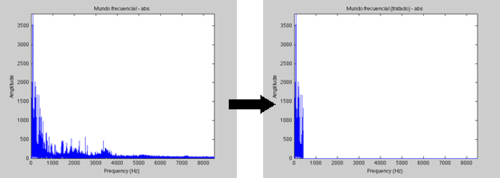
Esto se escuchará así:
Puede apreciarse que la voz del cantante casi ni se escucha. Si hubiéramos cogido frecuencias más bajas, no se hubiera escuchado nada, de hecho. Esto es debido a que la voz humana es capaz de emitir sólo en un rango de frecuencias (con pequeñas variaciones entre personas, un buen cantante será capaz de emitir muchas más frecuencias).
Todos estos ejemplos se han realizado utilizando MATLAB. Si tienes MATLAB instalado en tu ordenador, he aquí un ZIP con el código y algunos ejemplos para que tú mismo puedas investigar: DESCARGAR
Para concluir…
Con esto de las frecuencias también se explica que haya ciertos sonidos que nosotros no escuchemos y un perro sí. Para saber si vas a poder escuchar un sonido, puedes pasar la señal al mundo de Fourier y ver el rango de valores en los que esta señal es distinta de cero. Si toda la función (o parte de la misma) entra en el rango entre 200Hz y 18kHz, entonces (si tienes un oído normal) escucharás algo, pero si está fuera de este rango, por mucho que conectes al altavoz esa señal, no oirás nada (aunque el altavoz sí la estará emitiendo) y quizás un perro u otro animal, cuyo rango de frecuencias audibles es distinto al nuestro, sí esté escuchando sonidos.
He usado de ejemplo el sonido, pero cualquier señal puede transformarse a una señal de Fourier. La analogía más inmediata podría hacerse con el color. Podríamos empezar a “leer” señal electromagnética, después hacer su transformada y comprobar que si existe señal dentro del rango de frecuencias que nuestro ojo puede apreciar, entonces veríamos algo, sino sería invisible (aunque estar, estaría). En esto se basan las ondas electromagnéticas para ser invisibles: simplemente funcionan a unas frecuencias que nuestro ojo no puede apreciar. Son colores invisibles. Sobre este tema, aquí os dejo un vídeo muy divulgativo y fácil de ver que ahonda algo más en esta idea:
En definitiva, la transformada de Fourier, las frecuencias de las que tanto se oye hablar, no es más que trasladar cierta información de un mundo a otro, ya que en éste se ve todo más claro.